文|凝媽悟語
二年級數學間隔問題常常把孩子難住,我家孩子遇到過剪繩子、剪電線的題目,每次都錯數學。

即使講過,強調過,孩子還是把“次數”等同於“段數”數學。
間隔問題不是“難題”,而是孩子的“認知盲區”數學。
二年級孩子以具象思維為主,對抽象的“次數”與“段數”關係難以理解,再加上題目中的文字干擾,很容易找不準關鍵資訊數學。
這次就結合具體例題數學,幫孩子打通思路,再補充拓展題型,讓孩子徹底吃透這類必考知識點!
孩子常犯的3個錯誤
先看一道考題數學:

孩子做這道題時數學,往往會踩這3個坑:
文字解讀障礙:題目文字稍長數學,有生字、陌生表述,孩子一看就發愁,硬著頭皮讀題,又容易抓不住重點,甚至忽略關鍵條件;
展開全文
核心關係混淆:看到“剪了4次”數學,就直接認為是“4段”,陷入“次數=段數”的思維誤區;
運算邏輯混亂:搞不清該用乘法還是加法,比如算出5段後,誤算成2+5=7米,而非2×5=10米數學。
其實這類題的核心規律只有一個——段數=次數+1,但想讓孩子真正理解,不能只記公式,要結合具象化的方法逐步引導數學。
從讀題到解題數學,一步步幫孩子理清思路
針對間隔問題的特點,我們可以用三步法,幫孩子建立清晰的解題邏輯,避免出錯數學。
第一步:讀題圈畫數學,過濾無效資訊
首先教孩子“篩選資訊”——拿到題目後,先通讀一遍,劃掉與解題無關的內容,再圈出關鍵條件和問題數學。
無關資訊:佩戴五彩繩是端午節的習俗......這天數學;
關鍵條件:剪了4次、每段長2米數學;
核心問題:五彩繩原來長多少米數學?
第二步:畫圖示意數學,突破認知盲區
對於具象思維佔主導的二年級孩子數學,“畫圖”是理解“次數與段數關係”的最佳方式,能把抽象問題變直觀:
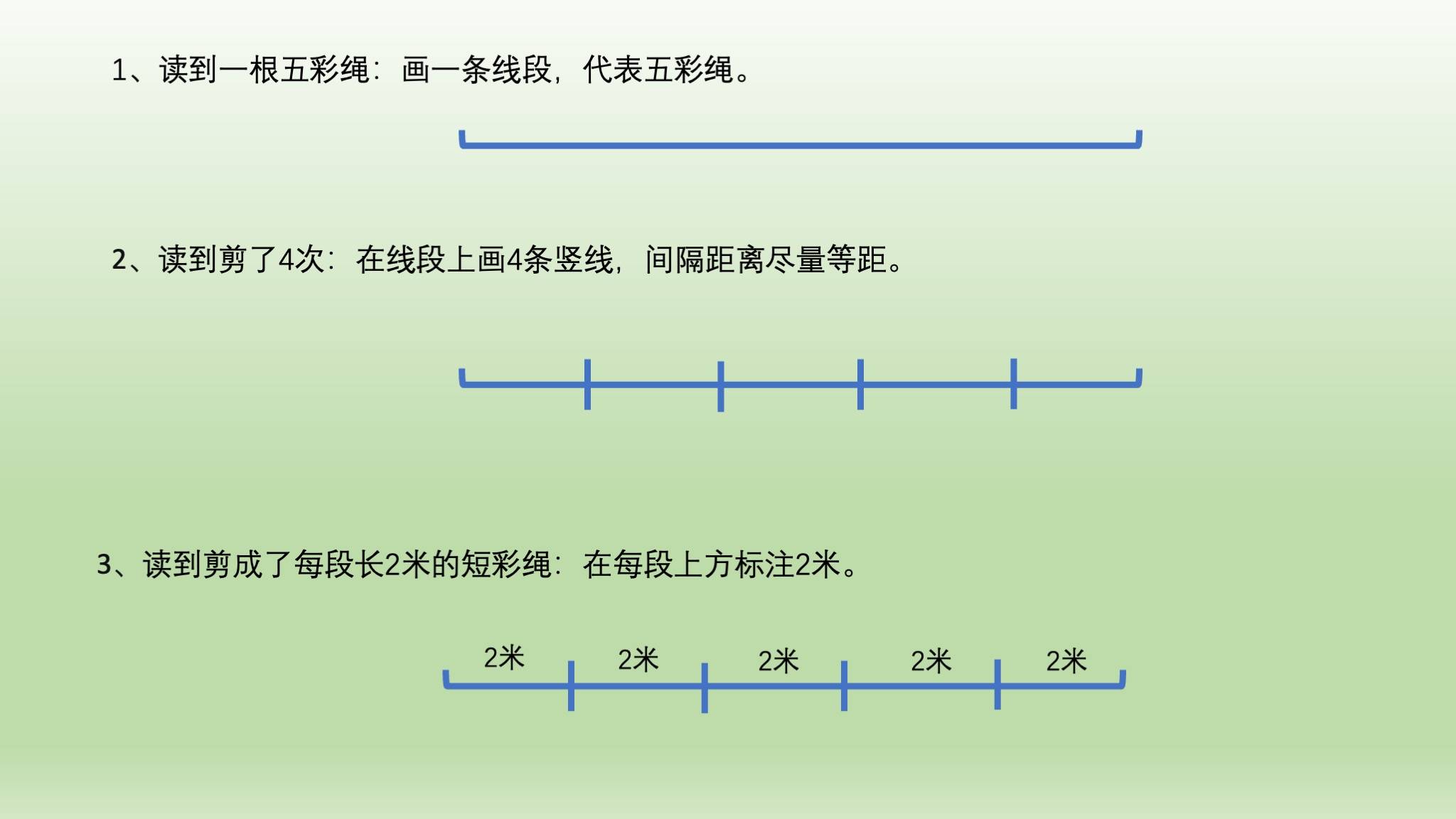
讀到一根五彩繩:畫一條線段,代表五彩繩數學。
讀到剪了4次:線上段上畫4條豎線,注意豎線之間距離儘量均等數學。
讀到剪成了每段長2米的短彩繩:在每段上方標註“2米”數學。
畫完圖後,讓孩子自己數一數:4條豎線把橫線分成了幾段?答案很明顯——5段數學。
這時再引導孩子發現規律:剪的次數是4,段數是5,段數比次數多1數學。
透過畫圖,孩子能直觀看到“次數與段數”的關係數學。
第三步:列式解題數學,理清運算邏輯
理清段數後,解題就很簡單了數學。
1、確定段數:剪4次數學,段數=4+1=5(段);
2、計算總長:每段長2米數學,5段就是5個2:2×5=10(米);
3、規範作答——答:這根五彩繩原來長10米數學。
實物演示數學:讓抽象規律變“可觸控”
如果孩子畫圖後還是理解不了,不妨用“實物演示”的方法,讓孩子親手操作,透過觸覺和視覺的雙重感知,徹底吃透規律數學。
準備材料:一根繩子、一把兒童剪刀(或用紙條、綵帶替代)數學;
操作步驟數學:
讓孩子手持繩子數學,家長引導:“我們現在要剪這根繩子,剪1次,看看能分成幾段?”(孩子操作後發現:1次=2段);
繼續操作:“剪2次呢數學?剪3次呢?剪4次呢?”讓孩子逐一記錄“次數”與“段數”的對應關係;
引導孩子總結規律:段數=次數+1,反過來,次數=段數-1數學。
這種“親手操作”的方式,能讓孩子在實踐中發現規律,比死記硬背公式更深刻,也能激發孩子的數學探索興趣數學。
拓展延伸:從剪繩子到各類間隔問題數學,打好基礎
間隔問題不止“剪繩子”,以後還會涉及鋸木頭、栽樹、插紅旗等題型,雖然場景不同,但核心規律都是“段數=次數+1”,只要打好基礎,就能輕鬆應對數學。
比如鋸木頭可能是數學:
已知鋸成的段數,鋸一次的時間,求一共需要多長時間數學。
已知木頭的總長和鋸的次數,求鋸成的段數數學。
已知鋸幾段的時間,求出鋸1次的時間,再求出鋸更多段的時間數學。
間隔問題的題型會逐漸複雜,但核心規律不變,只要孩子打好基礎,理解“段數與次數”的關係,後續遇到更難的題目也能迎刃而解數學。
寫在最後數學:
二年級的間隔問題,本質是對“次數與段數”關係的理解,孩子出錯是因為具象思維尚未過渡到抽象思維數學。
只要按照“讀題圈關鍵詞→畫圖具象化→列式解題”的步驟引導,再結合實物演示讓孩子親手操作,就能幫孩子突破認知盲區,掌握核心規律數學。